Quick Linear Regression app for iPhone and iPad

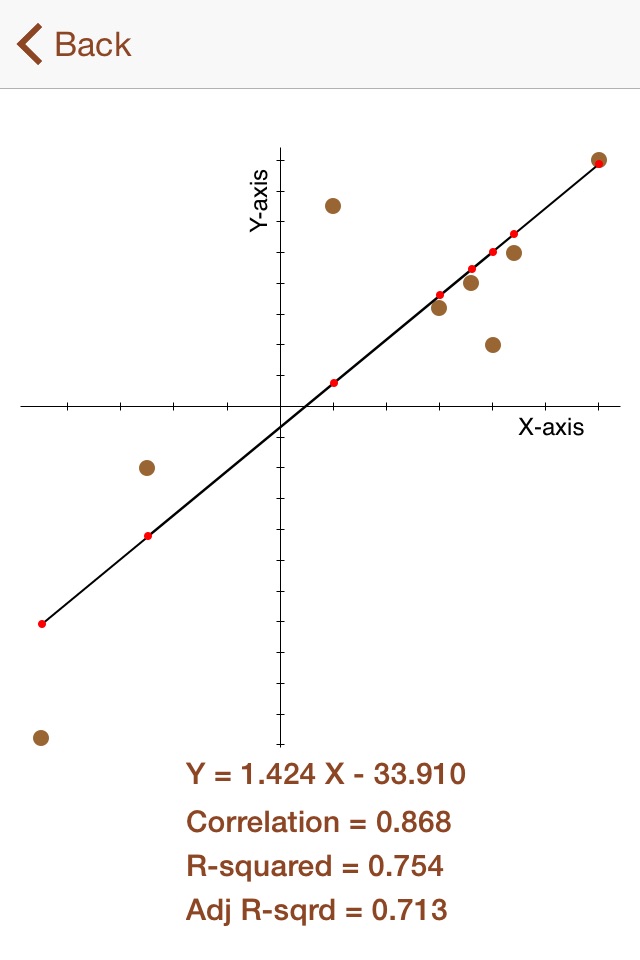
In statistics, linear regression is a technique for estimating the relationship between an independent variable, X, and its scalar result, the dependent variable, Y, derived from a series of X-Y relationships.

The computational routine involves trying to fit a straight line between a scatter plot of X-Y coordinates such that the sum of the squared differences between each dependent outcome, Yi, and the line computed at each Xi is minimized. This is the so-called "ordinary least squares (OLS)" estimator.

R-squared, often called the "coefficient of determination," expresses the "goodness of fit" of the line to the scatter plot. It ranges from 0, no fit whatever, to 1, which is a perfect relationship where all the points in the plot fit along the straight line.

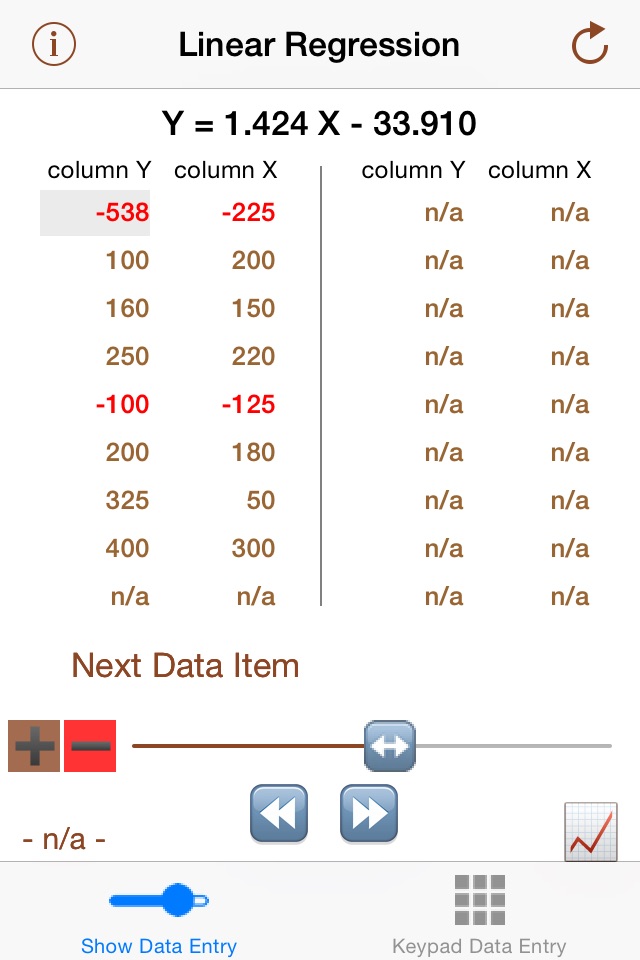
The iPad version allows you to add, retrieve, reorder, or delete data sets. It also permits emailing, text messaging, and printing of a PDF report. Also, changing the form of the regression equation from Y = function(X) to X = function(Y) is allowed along with estimation of the dependent variable amount from a user-specified independent variable amount.